The introduction of IFRS 9 marked a paradigm shift from the incurred loss model of IAS 39 to a forward-looking Expected Credit Loss (ECL) model. This change was a direct response to the delayed recognition of credit losses observed during the 2008 financial crisis. For portfolios of trade receivables, contract assets, and lease receivables, IFRS 9 provides a set of operational simplifications designed to reduce the implementation burden, yet it retains the core, challenging requirement to incorporate forward-looking economic information.

This blog explores a methodology that begins with the simplified provision matrix approach and enhances it with a non-parametric bootstrap technique. This method generates a distribution of potential future ECL outcomes, allowing for a defensible and auditable forward-looking adjustment. It provides a structured framework for what can be termed "governed expert judgment," helping firms move away from subjective, ad-hoc management overlays that have drawn supervisory scrutiny.

The Simplified Approach: Lifetime ECL as the Standard

Under IFRS 9, impairment is generally assessed using a three-stage model where the loss allowance is measured at either 12-month ECL (Stage 1) or lifetime ECL (Stage 2 and 3), depending on whether a significant increase in credit risk (SICR) has occurred since initial recognition. Recognising the operational complexity of tracking SICR for large volumes of relatively homogeneous and often short-term instruments, IFRS 9 provides a simplified approach. 

Under IFRS 9, the application of the simplified impairment approach is mandatory for certain financial assets. An entity must measure the loss allowance at an amount equal to Lifetime Expected Credit Losses (Lifetime ECLs) from initial recognition for both trade receivables or contract assets that do not contain a significant financing component (as per IFRS 9.5.5.15(a)) and for lease receivables (as per IFRS 9.5.5.15(b)). For trade receivables or contract assets that do contain a significant financing component, applying this simplified Lifetime ECL approach is an accounting policy choice (as permitted by IFRS 9.5.5.15).

Constructing the Baseline Provision Matrix

The most common tool for implementing the simplified approach is the provision matrix. This method allows an entity to calculate lifetime ECLs on a collective, or portfolio, basis. Building a robust baseline provision matrix involves two primary steps:

• Segmentation: The portfolio of receivables is segmented into groups with shared credit risk characteristics. The most common basis for segmentation is by days-past-due, creating aging buckets such as 'Current', '1-30 days past due', '31-60 days past due', and so on. However, IFRS 9 encourages more sophisticated segmentation where historical data shows significantly different loss patterns. This can include groupings by geographical region, product type, customer credit rating, or the nature of the customer (e.g., wholesale versus retail). The objective is to create pools of assets whose credit risk is expected to respond homogeneously to economic changes.
• Calculation of Historical Loss Rates: For each segment, an average historical loss rate is determined by observing the credit loss experience of past cohorts of receivables over their expected life. For example, to find the loss rate for the 'Current' bucket, an entity would analyse historical data to determine what percentage of receivables that were current at a given point in time ultimately defaulted over their entire lifecycle. The baseline ECL for the portfolio is then calculated by multiplying the gross carrying amount of receivables in each segment by its corresponding historical loss rate.

The Forward-Looking Imperative: Moving Beyond Historical Data

A provision matrix based solely on historical loss rates is not compliant with IFRS 9. The standard is unequivocal in its requirement for ECL measurement to be forward-looking. Paragraph 5.5.17 of IFRS 9 states that an ECL estimate must reflect:

• An unbiased and probability-weighted amount determined by evaluating a range of possible outcomes.
• The time value of money.
• Reasonable and supportable information about past events, current conditions, and forecasts of future economic conditions that is available without undue cost or effort.

This means the historical loss rates derived for the provision matrix serve only as a starting point. They represent the long-run average loss experience. This baseline must be adjusted to reflect the current economic context and expectations about the future. If forecasts indicate an economic downturn, the loss rates should be adjusted upwards; if a recovery is expected, they may be adjusted downwards.

This forward-looking requirement presents a significant analytical challenge. The provision matrix, while presented as a "simplification," is a double-edged sword. It simplifies the staging assessment by removing the need to track SICR. However, it simultaneously complicates the forward-looking adjustment. 

A sophisticated Probability of Default (PD) model might be built with a direct, statistically estimated regression link to a macroeconomic variable like GDP growth. In contrast, a simple provision matrix based on aging buckets has no inherent, direct link to such variables. In practice, this creates a gap: without a direct, data-driven link between loss rates and macroeconomic forecasts, firms must look to more advanced techniques to create a supportable and auditable forward-looking adjustment. 

Addressing this challenge is the central focus of this blog.

The Failure of Conventional Econometric Models

In practice, many entities – especially those managing large, granular portfolios spread across diverse industries and geographies – default to econometric models (such as regression analysis) to link historical loss rates to macroeconomic variables. However, this approach often fails. 

There are several reasons for this:

• Lack of Statistical Significance: The relationship between portfolio loss rates and high-level variables like GDP growth or national unemployment can be weak and statistically insignificant. The idiosyncratic risk within a diverse portfolio can easily overwhelm the systematic, macroeconomic signal.
• Instability: Any relationship that appears to exist in historical data may be unstable over time, breaking down during periods of structural economic change or unforeseen crises. A model calibrated on data from 2010-2019, for instance, may have offered little guidance during the unique circumstances of the COVID-19 pandemic.
• Non-Linearity: The impact of economic changes on credit losses is often non-linear. For example, a 2% drop in GDP may cause defaults to increase by a much larger magnitude than the decrease in defaults caused by a 2% rise in GDP. Standard linear regression models fail to capture these asymmetries.
• Data Limitations: Building a robust model requires a long, consistent time series of both portfolio loss data and macroeconomic variables, covering at least one full economic cycle. Many entities lack historical data of sufficient quality or length.

To bridge this model gap, many entities resort to the use of management overlays or post-model adjustments. These are typically expert-judgment-driven adjustments applied to the model output to account for factors the model does not capture, including forward-looking economic views. 

While overlays can be a necessary component of any modelling framework, their unstructured and subjective application is a significant source of regulatory concern.

To address these shortcomings, the objective must be to move away from purely subjective adjustments and towards a systematic, data-driven, and auditable process. The goal is not to eliminate expert judgment, but to structure and govern it. 

IFRS 9 requires an ECL that reflects a probability-weighted range of possible outcomes, not a single-point estimate based on one person's or one committee's view of the most likely future.

Therefore, a defensible framework for the forward-looking adjustment must be capable of quantifying the uncertainty surrounding future economic conditions and translating that uncertainty into a robust and supportable adjustment to the baseline ECL. This is where the bootstrap technique offers a powerful solution. It provides a framework for what can be termed "governed expert judgment."

Applying the Bootstrap Technique

Bootstrapping is a computational, statistical method that estimates the sampling distribution of a statistic by repeatedly resampling from an original observed dataset. Its primary advantage is that it is non-parametric; it makes no assumptions about the underlying distribution. Instead, it relies on the empirical distribution of observed data.

The following step-by-step guide outlines how the bootstrap technique can be integrated with a provision matrix to derive a robust, data-driven forward-looking ECL adjustment.

Step 1: Calculate Baseline ECL and Historical Flow Rates 

The process begins with establishing a baseline from long-run historical data.

• Compile Historical Flow Rates: Gather a time series of historical data on how receivable balances "flow" or "roll" between aging buckets from one period to the next. This creates a series of historical flow-rate matrices.
• Calculate Weighted Average Flow Rates: Determine the long-run weighted average flow rate for each possible transition (e.g., from “Current” to “1-30 days past due”). This average represents the expected flow rate under long-run conditions.
• Calculate Baseline ECL: Use these average flow rates to simulate the lifecycle of a cohort of receivables, thereby calculating the long-run average lifetime loss rate for each aging bucket. Applying these average loss rates to the current gross carrying amounts computes the baseline ECL.

Step 2: Calculate Pearson Residuals for Historical Flow Rates 

This step quantifies the historical volatility around the average. The key assumption is that the observed flow rates at each historical reporting date represent a sample from a random distribution.

• For each flow rate in each aging band for each historical period, a Pearson residual is calculated. The Pearson residual is the scaled difference between the actual, observed flow rate for that period and the long-run weighted average flow rate calculated in Step 1.
• This process creates a pool of historical residuals for each flow rate transition. Each residual represents a historical, period-specific "shock" (either positive or negative) to the average flow rate.

Step 3: Generate Scenarios by Bootstrapping Pearson Residuals 

This is the core resampling step of the process. To generate one future scenario, a set of residuals is created by randomly drawing with replacement from the pool of historical Pearson residuals calculated in Step 2. One residual is drawn for each flow rate in the matrix.

Step 4: Construct Resampled Flow Rates and Calculate Scenario ECL 

For each of the thousands of simulations runs, a unique set of future flow rates is constructed and the corresponding ECL is calculated.

• A new "bootstrapped" flow rate is constructed for each transition by adding the randomly selected Pearson residual (from Step 3) to the long-run weighted average flow rate (from Step 1). This creates a full matrix of simulated future flow rates.
• Using this new flow rate matrix, the corresponding lifetime loss rates for each aging bucket are calculated.
• These new loss rates are then applied to the current portfolio balances to calculate the total ECL for that single scenario.

Step 5: Incorporate Forward-Looking Judgemental Overlays 

The distribution of ECLs generated from the previous steps reflects the portfolio's historical volatility, but it may not fully capture all reasonable and supportable forward-looking information, particularly for novel risks or specific economic forecasts. This step introduces governed expert judgement through overlays. Overlays are necessary when management has a view on future conditions that is not adequately represented in the historical data used for the bootstrap. This could include the impact of new legislation, a geopolitical event, or a pandemic for which there is no historical precedent in the data.

• Weighted Resampling: A structured approach is to adjust the probabilities of the bootstrapped scenarios. If a severe downturn is forecast, the historical periods corresponding to past recessions (identified by their large negative residuals) can be given a higher weight in the resampling process. This embeds the forward-looking view directly into the statistical process.
• Post-Model Overlay: An explicit, documented adjustment can be applied after the initial bootstrap distribution is generated. This is particularly useful for novel risks. The overlay should be quantified based on a defined, severe-but-plausible scenario, its estimated impact, and its assigned probability. For example: 
  Overlay Adjustment = (ECL under Defined Scenario - Mean Bootstrap ECL) * Probability of Scenario. This adjustment should be applied at a granular level (e.g., to specific risk parameters or portfolio segments) rather than as a single top-level adjustment to the final ECL number, a practice that has drawn regulatory criticism.

Step 6: Generating the Final ECL Distribution. 

The overlay logic from Step 5 is applied to the results of Step 4 to generate a final, forward-looking distribution of ECL outcomes. This process is repeated a large number of times (typically 1,000 to 10,000) to produce a distribution of thousands of possible ECL outcomes. This distribution represents the range of potential ECLs and their likelihoods, reflecting the portfolio's inherent historical volatility.

Step 7: Determine the Final ECL Provision 

The final step is to derive the required ECL provision from the generated distribution.

• The mean of the thousands of ECL outcomes from the bootstrap distribution represents the unbiased, probability-weighted ECL required by IFRS 9. This is the amount that should be recognised as the final loss allowance for the portfolio.
• The bootstrap distribution also provides valuable information for risk management and disclosure. The 2.5th and 97.5th percentiles of the distribution can be used to construct a 95% confidence interval for the ECL.

The following tables provide an illustration of the inputs and outputs of this process.

Table 1: Illustrative Baseline Provision Matrix Calculation

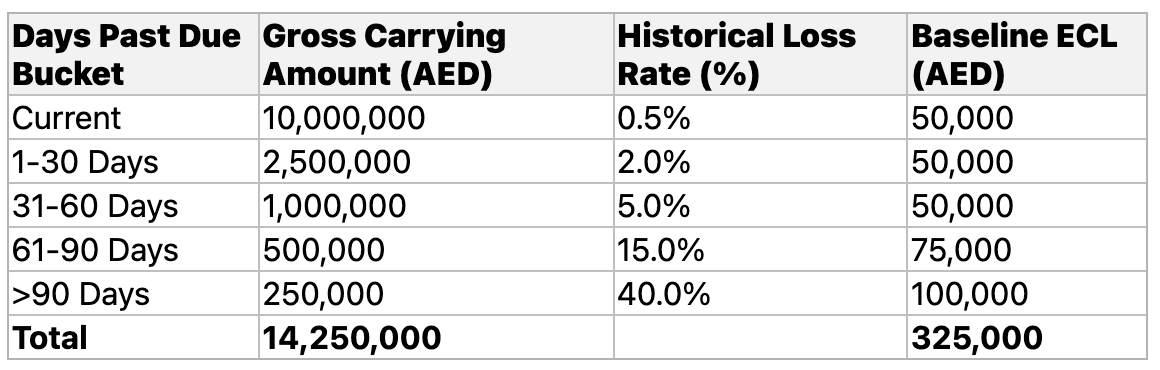
Table 2: Sample Output of Bootstrap Simulation and Final ECL Calculation

Part A: Summary of Bootstrap ECL Distribution

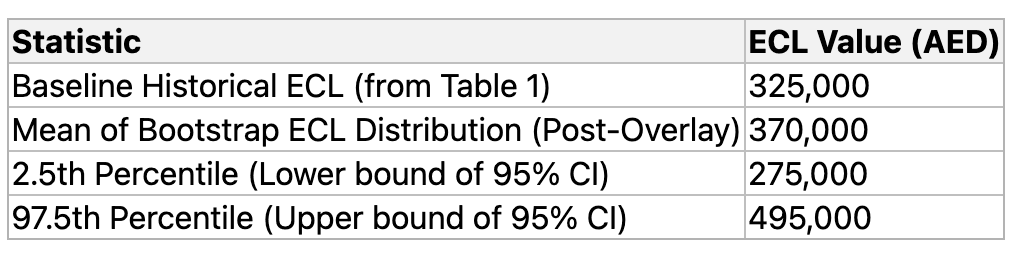
Part B: Final ECL Calculation

Validating the Approach within the IFRS 9 Framework

The bootstrap framework is explicitly designed to meet the core requirements of IFRS 9:

• Unbiased and Probability-Weighted Outcomes: Paragraph 5.5.17(a) of IFRS 9 requires the ECL to reflect "an unbiased and probability-weighted amount that is determined by evaluating a range of possible outcomes". The bootstrap process achieves this by generating thousands of potential outcomes based on historical volatility. The final ECL, calculated as the mean of this distribution, is the mathematical definition of a probability-weighted expected value, thereby avoiding a biased estimate based on a single best- or worst-case scenario. This aligns with paragraph B5.5.42, which clarifies that while a complex analysis is not always needed, the method must capture a range of possible outcomes.
• Forward-Looking Information: The standard mandates the use of "reasonable and supportable information... about... forecasts of future economic conditions" (Paragraph 5.5.17(c)). The bootstrap methodology incorporates this in two ways. First, the resampling of historical data itself is a form of forward-looking estimation; it implicitly assumes that the full range of volatility and economic conditions experienced in the past is a reasonable and supportable basis for estimating the range of uncertain future outcomes. Second, the framework explicitly incorporates specific forecasts through the governed overlay process (Step 5), where expert judgment about future conditions is used to adjust the historically derived distribution, ensuring the final ECL reflects current expectations.
• Point in Time estimates: The bootstrap methodology is fundamentally a PiT approach. It does not produce a single long-run average. Instead, by resampling recent historical data, it naturally produces a wider, more uncertain distribution of future scenarios if the recent past has been volatile. If the economy enters a downturn, the resampling process will be drawing from historical data that contains more negative outcomes, naturally skewing the distribution towards more pessimistic results. This makes the resulting ECL estimate highly responsive and sensitive to changing economic conditions, directly fulfilling the PiT requirement and avoiding the forced stability of a Through the Cycle (TTC) approach.

From Simplification to Governance in IFRS 9

Meeting the forward-looking principles of IFRS 9 requires a fundamental shift from static, historical-based calculations to a dynamic, probability-weighted framework. The bootstrap methodology detailed in this blog provides a powerful tool to achieve this, transforming the provision matrix from a simple starting point into a robust engine for generating defensible, forward-looking Expected Credit Loss provisions through a process of governed expert judgment.

Practitioners must remain wary of common pitfalls in ECL provisioning. These include an over-reliance on unadjusted historical loss rates; the failure of conventional econometric models to capture non-linear risks; and the use of subjective, unstructured management overlays that attract significant auditor and regulatory scrutiny. The "simplified approach" itself presents a hidden complexity: it removes the burden of staging but amplifies the challenge of creating a supportable, forward-looking adjustment.

In an environment of heightened economic uncertainty and regulatory focus, particularly in dynamic regions like the UAE and KSA, an auditable and robust ECL framework is no longer optional. At Lux Actuaries, licensed by the UAE's Securities and Commodities Authority (SCA) to perform financial consulting and advisory services, we provide end-to-end support for your IFRS 9 requirements - from initial ECL model design and validation to implementing advanced statistical techniques and delivering ongoing managed services. 

Looking to strengthen your IFRS 9 ECL provisioning? Contact us to explore how Lux Actuaries can support your framework with expert guidance and practical solutions.